Thales von Milet

Thales von Milet ist der erste namentlich bekannte griechische Philosoph und Naturwissenschaftler und gilt als einer der Begründer von Wissenschaft und Philosophie überhaupt. Er lebte um das 6. Jahrhundert vor Christus in Kleinasien und brachte durch Reisen nach Ägypten orientalische Kenntnisse in Astronomie und Mathematik nach Griechenland. In der Mathematik gehen verschiedene elementargeometrische Sätze auf ihn zurück. Der bekannteste davon ist der nach ihm benannte Satz des Thales, nach welchem der Umfangswinkel über dem Durchmesser eines Kreises ein rechter Winkel ist.

Was volbrachte Thales von Milet?

-Bekannt wurde er, da er erfolgreich eine Sonnenfinsternis für das Jahr 585 v. Chr. voraussagte

-Er unternahm eine Reise nach Ägypten um sein wissen weiterzubilden.
In Ägypten wurde er dadurch bekannt dass, er die Höhe einer Pyramide berechnete nur mithilfe eines Stockes (die Länge wahr bekannt) und seinem eigenem Schatten

-Das bekannteste und eins der letzten Überreste von Thales von Milet ist der Satz des Thales der nach ihm benannt wurde

Der Satz des Thales

Konstruiert man einen Halbkreis, zeichnet man den Durchmesser ein, nimmt die Eckpunkte des Durchmesser und des Halbkreises und setzt man einen dritten Punkt auf den Halbkreis und verbindet man diese drei Punkte somit erhält man im Winkel vom Halbreis (Gamma) immer einen rechten Winkel



Und wie ihr anhand diesem Bild sehen könnt ist es egal wo ihr den Punkt C setzt, ihr erhaltet immer einen rechten Winkel (90 Crad)



Warum ist das so ?
Beweis: 1 (gleichschänkliches Dreieck)

Wir zeichnen den Mittelpunkt ein und wissen das von M zu Punkt A der Abstand r ist, von Punkt C und M ist der Abstand r und von C und M ist der Abstand auch r. Danach zeichnen wir die Linie von Punkt M und C ein. Damit erhalten wir ein gleichschenkliges Dreieck.



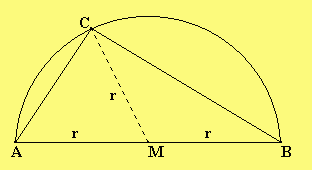
Nun zeichnen wir alle gleichen Winkel ein :



Wir wissen das die Innenwinkelsumme eines Dreiecks immer 180° hat. Somit muss auch unser Dreieck hier 180° haben. Also addieren wir jetzt mal alle Winkel

α + β + (α + β) = 180°

Die Winkel hier in der Klammer ist in diesen Fall der Punkt C
Diese Gleichung können wir auch anderst schreiben

2α + 2β = 180°

Also können wir auch die 2 Ausklammern

2(α + β) = 180°

Nun Dividieren wir die Gleichung durch 2

(α + β) = 90°

Und wie ich vorhin bereitsgesagt habe die Winkel (α + β) in der Klammer ist Punkt C Somit haben wir bewiesen das in Punkt C einen rechter Winkel (90°) ist.

http://firebook.twoday.net/stories/satz-des-thales